How to make money in Natural Gas with Python

Posted: 2024-01-25

In one of the previous posts, we were talking about simple gas storage model as a business opportunity. That model has one serious drawback: it does not take injection and withdrawal ratchets.

An inventory ratchet means different maximum daily injection or withdrawal quantity depending on the amount of gas in storage. The picture below shows injection ratchets as a function of storage level.

Previous excel model has limited features and also Excel’s solver convergence is not great. Industry use requires a model that would closely mimic reality which means a need to use nonlinear functions in constraint definition. On the top of that, the problem is a Mixed Integer Programming which forces to use specialized solvers.

One of them with a decent quality is CBC solver from fantastic COIN-OR project. We’re going to sprinkle the model with a bit of Python and bake it in Jupyter to get this notebook.

There are some interesting results. When injection ratchet is constant at 2000 Dth per day, the storage peaks 100,000 in 2nd and 3rd month. Additionally, withdrawal strategy is trying to monetize small peak during summer demand for cooling power.

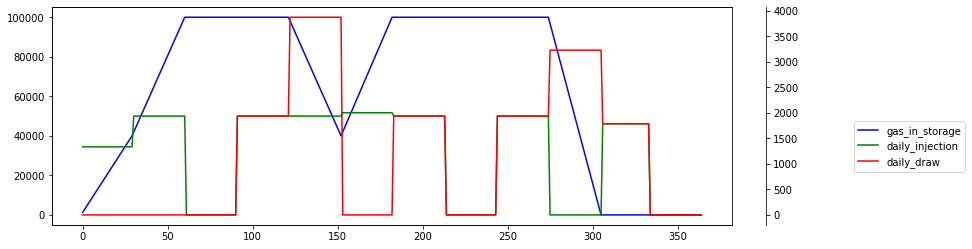
Not much change when the ratchet is reduced to 1000 Dth.

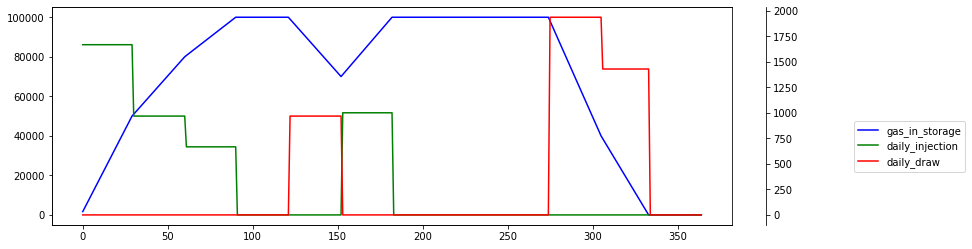
However, ratchet reduction by 75% at half storage shows rather dramatic injection profile. This time storage peaks roughly in 6th month.

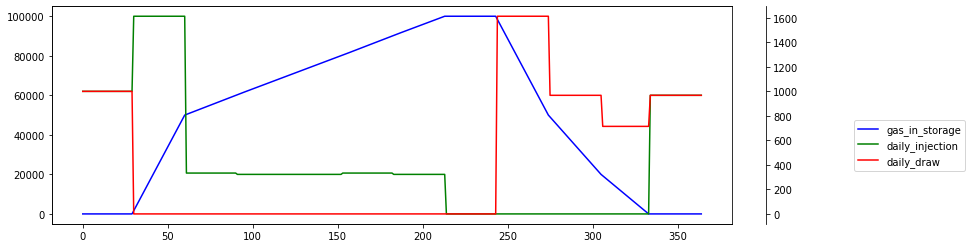
This model is still very basic because it skips discounting and costs. Nonetheless, ability to specify fairly complex constraints, combined with python and MIP solvers allow for very powerful scenario analysis.

There is one more draw back of the model. It does not take volatility into account, but this is a material for the next post.

Image by Kevin Schneider from Pixabay

Help! My python code is slow

Posted: 2023-10-22

TLDR: List comprehension is faster then append

Ok, so this isn’t a picture of a python snake (this is a boa constrictor), but it is the same story with append vs yield: they both kind of work in the same manner.

Most popular patterns in Python to create a list of widgets, can be summarised into these two categories: - for loop and then append on the list:

    l = []
    for x in sequence:
        y = do_something( x )
        l.append( y )

• list comprehension with generator expresion

  def gen( sequence ):
      for x in sequence:
          yield do_something( x )
  
  l = [ x for x in gen( sequence ) ]
  

What is interesting however is that list comprehension is much faster. Here’s the chart to show to ilustrate the performance of these two solutions

– insert chart of both – tested with python 3.6 and cpu

def do_something( x ):
	return x

def m1(sequence):
	l = []
	for x in sequence:
		y = do_something( x )
		l.append( y )

def gen( sequence ):
	for x in sequence:
		yield do_something( x )

def m2(sequence):
    l = [ x for x in gen( sequence ) ]


sizes = [ 1000, 10000, 100000, 1000000, 10000000, 100000000 ]


def iter(arr):
	for s in sizes:
		seq = range(s)
		r1 = %timeit -o m1(seq)
		r2 = %timeit -o m2(seq)
	
		yield (s, r1, r2)

results = [ i for i in iter(sizes) ]

import matplotlib.pyplot as plt                                                                                                                      

x = sizes
y1 = [ i[1].average for i in results]
y2 = [ i[2].average for i in results]
plt.loglog( x, y1, x, y2 )

Photo by David Clode on Unsplash