How to make money in Natural Gas with Python

Posted: 2024-01-25

In one of the previous posts, we were talking about simple gas storage model as a business opportunity. That model has one serious drawback: it does not take injection and withdrawal ratchets.

An inventory ratchet means different maximum daily injection or withdrawal quantity depending on the amount of gas in storage. The picture below shows injection ratchets as a function of storage level.

Previous excel model has limited features and also Excel’s solver convergence is not great. Industry use requires a model that would closely mimic reality which means a need to use nonlinear functions in constraint definition. On the top of that, the problem is a Mixed Integer Programming which forces to use specialized solvers.

One of them with a decent quality is CBC solver from fantastic COIN-OR project. We’re going to sprinkle the model with a bit of Python and bake it in Jupyter to get this notebook.

There are some interesting results. When injection ratchet is constant at 2000 Dth per day, the storage peaks 100,000 in 2nd and 3rd month. Additionally, withdrawal strategy is trying to monetize small peak during summer demand for cooling power.

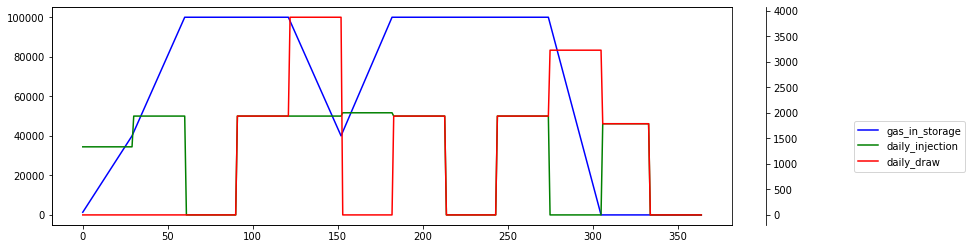
Not much change when the ratchet is reduced to 1000 Dth.

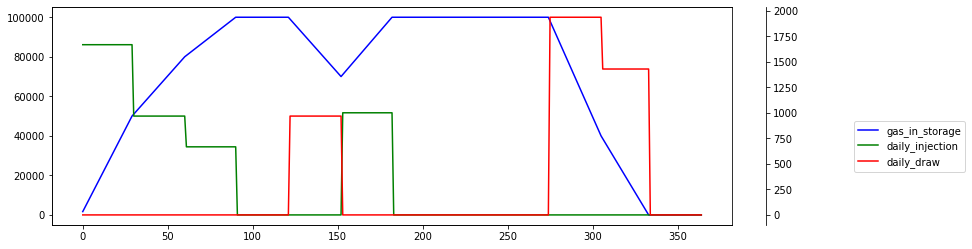
However, ratchet reduction by 75% at half storage shows rather dramatic injection profile. This time storage peaks roughly in 6th month.

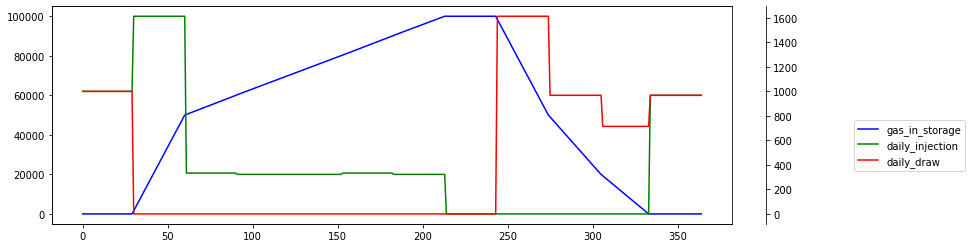
This model is still very basic because it skips discounting and costs. Nonetheless, ability to specify fairly complex constraints, combined with python and MIP solvers allow for very powerful scenario analysis.

There is one more draw back of the model. It does not take volatility into account, but this is a material for the next post.

Image by Kevin Schneider from Pixabay

How to make money in Natural Gas with Excel

Posted: 2023-10-20

One of the strategies is to buy cheap summer gas, store it for few months, and sell as expensive winter gas. Easily said than done. But how much should you pay for the storage facility and how to hedge the risk?

In this post we are going to review a simple gas storage model with static replication. This is an educational exercise and it is designed for simplicity.

Natural Gas storage is a critical function that operators use to balance the demand and supply especially during summer / winter seasons. Historically the heating demand for Natural Gas during winter is much higher than summer power burn and industrial demand which is reflected in the gas forward curve.

As mentioned earlier, winter Natural Gas demand is typically higher than available supply hence winter prices are also typically higher than summer prices. Gas storage owners use this phenomenon to buy “cheap” gas during summer months and sell during more expensive winter months.

Let us look at a simple storage model with 1y firm contract with no ratchets, no injection, draw and financing costs and no bid-offer or locational spreads. The hedge will follow static replication method, which means we are not taking volatility into consideration just price levels.

To solve optimization problem, we need to first define a target function. We are going to maximize revenue by buying gas and selling it later. The schedule will be subject to constraints: - maximum storage level cannot be greater than 100,000 dekatherms - maximum daily injection rate cannot be greater than 2,000 dekatherms - maximum daily withdrawal rate cannot be greater than 4,000 dekatherms

This formula describes our target function: $$ \max \sum Q{ij}(P{j}-P{i}) $$ , where: $Q{ij}$ means we are buying $Q$ dekatherms in month $i$, keeping it in storage and selling the same amount in month $j$. $P{i}$ and $P{j}$ are respective purchase and sell prices.

We are going to skip constraints for brevity, the target formula and constraints are implemented in attached Excel sheet.

Using Excel solver shows that we can make revenue of USD 39,520 so if storage costs less than that we can make some profit.

Here is calculated hedging plan. For example, we need to buy 3 April’21 contracts at price 2.921 and sell 3 Jan’22 contracts at price 3.294 to hedge the P&L.

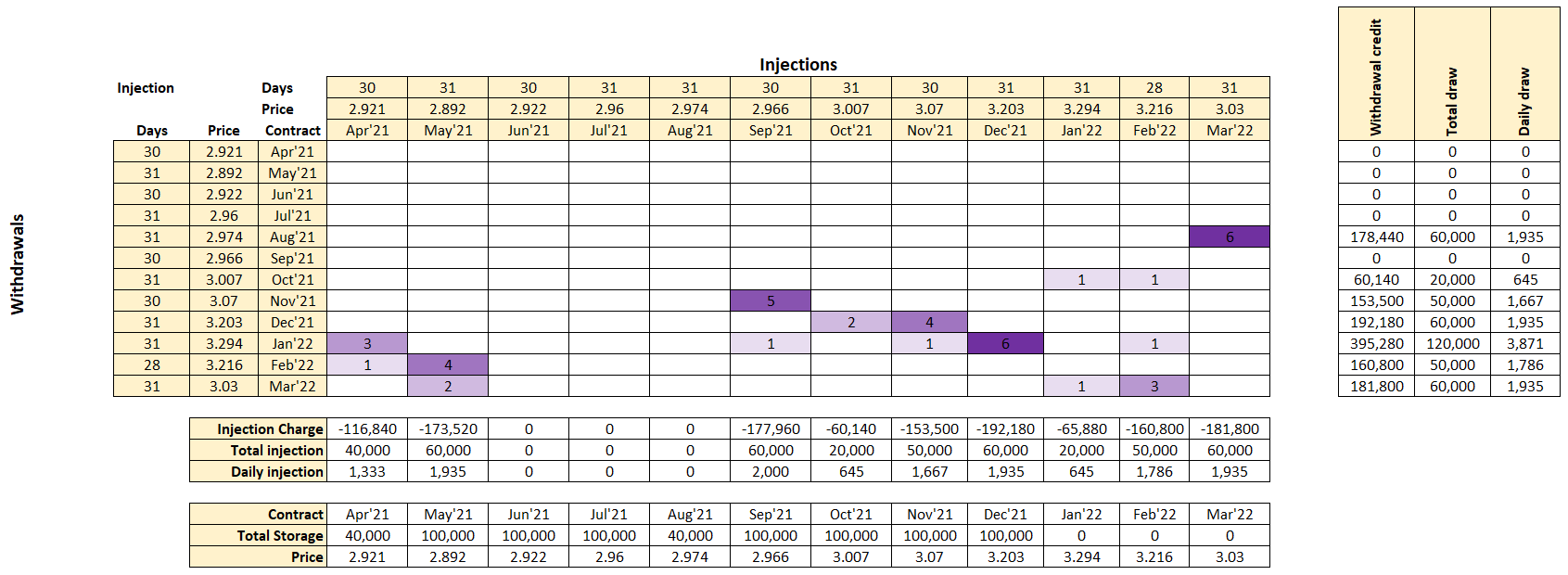
This chart shows amount of gas in storage for calculated plan vs the forward prices. The solver did an excellent job and constrained maximum storage level to 100,000 as was required.

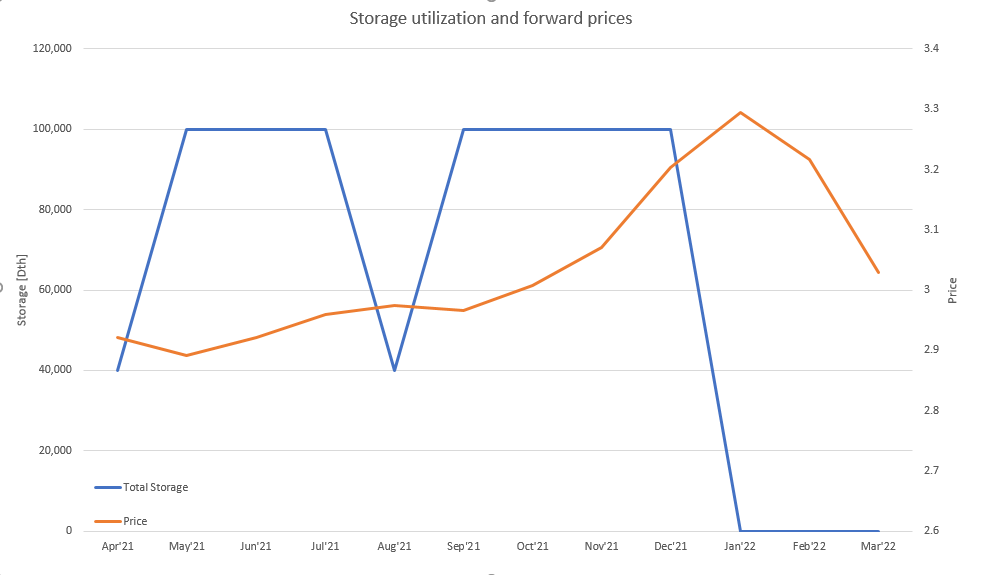
Photo by Josh Appel on Unsplash